ByteCTF re moderncpp 题解

ctf 10 minutes read (About 1527 words)

首发于先知

题目本身并不难，最大的难点在于要逆C++的数据结构，导致程序的逻辑难以理解。

Analysis

main函数位于0x402954，主要的逻辑就是输入、进行检查、初始化、数据处理以及最后的对比。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
int __cdecl main(int argc, const char **argv, const char **envp)
{
  __int64 v3; // rax
  __int64 v4; // rbx
  __int64 v5; // rbx
  void (__fastcall *v6)(char *, __int64, __int64); // rbx
  __int64 v7; // rax
  __int64 v8; // rax
  __int64 v9; // rax
  char v11[16]; // [rsp+0h] [rbp-C0h] BYREF
  char v12[16]; // [rsp+10h] [rbp-B0h] BYREF
  char answer[32]; // [rsp+20h] [rbp-A0h] BYREF
  char input[47]; // [rsp+40h] [rbp-80h] BYREF
  char v15; // [rsp+6Fh] [rbp-51h] BYREF
  char v16[16]; // [rsp+70h] [rbp-50h] BYREF
  char v17[16]; // [rsp+80h] [rbp-40h] BYREF
  __int64 v18; // [rsp+A0h] [rbp-20h]
  __int64 v19; // [rsp+A8h] [rbp-18h]

  sub_4257A0(input);
  nullsub_7(&v15);
  sub_427EC0(answer, &dword_536800, 40LL, &v15); //最终结果
  nullsub_9(&v15);
  v3 = sub_41F910(&stdout, "input:");
  ((void (__fastcall *)(__int64))sub_41F2C0)(v3);
  sub_40BDC0(&stdin, input); //输入
  v4 = malloc(64LL);
  sub_4010A0(v4);
  v18 = v4;
  v5 = malloc(64LL);
  sub_4010A0(v5);
  v19 = v5;
  check_1(input); //检查以及初始化
  (*(void (__fastcall **)(char *, __int64, char *))(*(_QWORD *)v18 + 8LL))(v16, v18, input);
  sub_404334(v12, v16);
  sub_403E24(v16);
  v6 = *(void (__fastcall **)(char *, __int64, __int64))(*(_QWORD *)v19 + 8LL);
  v7 = sub_404EF6(v12);
  v6(v17, v19, v7);
  sub_404334(v11, v17);
  sub_403E24(v17);
  v8 = sub_404EF6(v11);
  if ( (unsigned __int8)sub_404F07(v8, answer) ) //比较
    v9 = sub_41F910(&stdout, "congrats!");
  else
    v9 = sub_41F910(&stdout, "try again.");
  ((void (__fastcall *)(__int64))sub_41F2C0)(v9);
  sub_403E24(v11);
  sub_403E24(v12);
  sub_4258C0(answer);
  sub_4258C0(input);
  return 0;
}

0x4027D5处函数(check_1)先对输入进行了检查，要求长度为41且格式为bytectf{*****}。

1

接下来进行了部分初始化操作，输出了一句似乎没什么用的话，然后进行了编码操作。

第一步是在0x401414函数处生成字母表

该处操作在内存中生成了一个字母表abcdefghijklmnopqrstuvwxyz0123456789!@#%^&*()_+-=[]{};，接着在该函数中调用0x4018D6处函数，生成与字母表长度相同的一个整数数组，生成的规则如下：

第二步在上述函数中调用0x401C86处函数，主要进行的操作就是将上面生成的两个进行一一对应的组合

第三步是经过对数据的一些预处理操作之后，在sub_4015EE(gen_code)内对字母表中的字母进行编码

很像一棵树，先添“0”，遍历左子树，然后添“1”，遍历右子树，很明显利用预先构造好的树对字符进行0-1编码。编码结束之后对输入进行处理。

第一步处理很简单，对输入进行逐字节编码，拼接在一起，然后8位一组转化为int。

可以发现是高位在前，低位在后

该部分经过多次调试可以发现，每一个字母为不等长0-1编码，且每次编码固定，如果不确定是什么编码方式的话也可以使用调试的方式，通过输入不同的字符来查找对应的编码。但实际上很容易想到这是Huffman编码。

后面的处理是加密，在0x4024A4处，根据特征值0x9E3779B9或者使用findcrypt插件可以很容易发现这是tea加密

明文为刚刚进行编码过的数据，对该函数交叉引用很快就可以找到key

继续回到main函数，加密的结果与最开始拷贝的0x536800处的40个字节进行对比，相同则正确。

Solution

先解密tea得到编码后的结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <stdio.h>
#include <stdint.h>

void decrypt(uint32_t *v, uint32_t *k)
{
    uint32_t v0 = v[0], v1 = v[1], sum = 0xC6EF3720, i;
    uint32_t delta = 0x9e3779b9;
    uint32_t k0 = k[0], k1 = k[1], k2 = k[2], k3 = k[3];
    for (i = 0; i < 32; i++)
    {
        v1 -= ((v0 << 4) + k2) ^ (v0 + sum) ^ ((v0 >> 5) + k3);
        v0 -= ((v1 << 4) + k0) ^ (v1 + sum) ^ ((v1 >> 5) + k1);
        sum -= delta;
    }
    v[0] = v0;
    v[1] = v1;
}

int main()
{
    uint32_t v[10] = {0x0C5D3669F, 0x0B917171A, 0x0B4B37B19, 0x0AE80C5F, 0x8D80307F, 0x21522880, 0x34D80589, 0x0DE6C83D1, 0x59B73618, 0x0C6E65D35}, k[4] = {0x62797465, 0x2D637466, 0x77656C63, 0x6F6D657E};
    for (int i = 0; i < 5; i++)
    {
        uint32_t tmp_v[]={v[2*i],v[2*i+1]};
        decrypt(tmp_v, k);
        printf("%x,%x,", tmp_v[0], tmp_v[1]);
    }

    return 0;
}
// d869f00c,62fb324a,ccca48e,e56322c0,5e07fdb6,8dc6fee6,ad518dfd,14fa68e4,78

按照小端序转换为字节后，继续转换为8位二进制字符串拼接，从头开始向后遍历，在表中找到对应的字母后调整开头位置，继续向后遍历，Huffman编码保证了这样做结果的唯一性。字母表使用Huffman编码的方式生成会更快，但是手动调试出来对于程序分析的难度会较低，是个比较讨巧的办法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
class Node():
    def __init__(self, name=None, value=None):
        self.name = name
        self.value = value
        self.right = None
        self.left = None


class HuffmanTree():
    def __init__(self, arr):
        self.charset = {}
        self.nodes = [Node(values[0], values[1])
                      for values in arr]
        while len(self.nodes) != 1:
            self.nodes.sort(key=lambda node: node.value)
            p = Node(value=(self.nodes[0].value +
                     self.nodes[1].value))
            p.left = self.nodes.pop(0)
            p.right = self.nodes.pop(0)
            self.nodes.append(p)
        self.root = self.nodes[0]

        self.Code = list(range(60))

    def HuffmanCode(self, tree, length):
        node = tree
        if (not node):
            return
        elif node.name:
            result = ''
            for i in range(length):
                result += str(self.Code[i])
            self.charset[node.name] = result
            return
        self.Code[length] = 0
        self.HuffmanCode(tree.left, length + 1)
        self.Code[length] = 1
        self.HuffmanCode(tree.right, length+1)

    def GenCode(self):
        self.HuffmanCode(self.root, 0)


alphabet = 'abcdefghijklmnopqrstuvwxyz0123456789!@#%^&*()_+-=[]{};'
arr = []
for i in range(54):
    arr.append((43*(127+i)) % 233)
char_weights = list(zip(alphabet, arr))
tree = HuffmanTree(char_weights)
tree.GenCode()

# check
charset = {
    'b': '00001',
    'y': '10011',
    't': '11000',
    'e': '0011010',
    'c': '01110',
    'f': '010010',
    '{': '10001',
    'a': '100101',
    'd': '11011',
    'g': '111011',
    'h': '01000',
    'i': '10110',
    'j': '00110111',
    'k': '1111010',
    'l': '110010',
    'm': '00011',
    'n': '10000',
    'o': '10100011101',
    'p': '0110011',
    'q': '011000',
    'r': '111110',
    's': '01011',
    'u': '11110110',
    'v': '000001',
    'w': '111000',
    'x': '00101',
    'z': '101000110',
    '0': '1110010',
    '1': '100100',
    '2': '111111',
    '3': '01101',
    '4': '11010',
    '5': '11110111',
    '}': '1010001111',
    '6': '001100',
    '7': '111010',
    '8': '00111',
    '9': '10101',
    '!': '00110110',
    '@': '1110011',
    '#': '101001',
    '%': '00010',
    '^': '01111',
    '&': '10100011100',
    '*': '0110010',
    '(': '010011',
    ')': '111100',
    '_': '01010',
    '+': '10111',
    '-': '10100010',
    '=': '000000',
    '[': '110011',
    ']': '00100',
    ';': '1010000'

}

assert(charset == tree.charset)

new_dic = dict(zip(tree.charset.values(), tree.charset.keys()))
# d869f00c,62fb324a,ccca48e,e56322c0,5e07fdb6,8dc6fee6,ad518dfd,14fa68e4,78
target = [0x0c, 0xf0, 0x69, 0xd8, 0x4a, 0x32, 0xfb, 0x62, 0x8e, 0xa4, 0xcc, 0x0c, 0xc0, 0x22, 0x63,
          0xe5, 0xb6, 0xfd, 0x07, 0x5e, 0xe6, 0xfe, 0xc6, 0x8d, 0xfd, 0x8d, 0x51, 0xad, 0xe4, 0x68,
          0xfa, 0x14, 0x78]
f = ''.join([bin(i)[2:].rjust(8, '0') for i in target])

i = 0
j = 5
while j < len(f):
    tmp = f[i:j]
    if new_dic.get(tmp):
        print(new_dic[tmp], end='')
        i = j
        j += 5
    else:
        j += 1

需要注意的是这里生成Huffman编码的时候，相同数值使用不同的排序算法可能会有不同的顺序，例如使用python的sort算法时，倒序的方式生成的编码与题目中生成的不同，有可能需要多尝试几次。

#ctf #re #ByteCTF
L3HCTF re double-joy 题解 wp-5space-2021

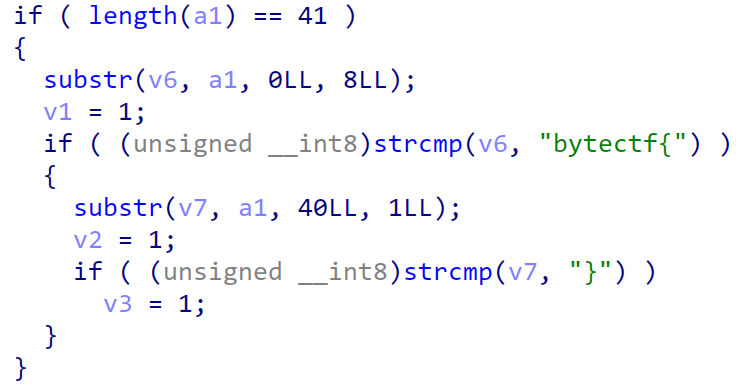
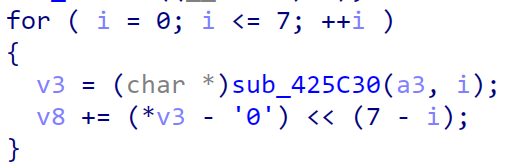
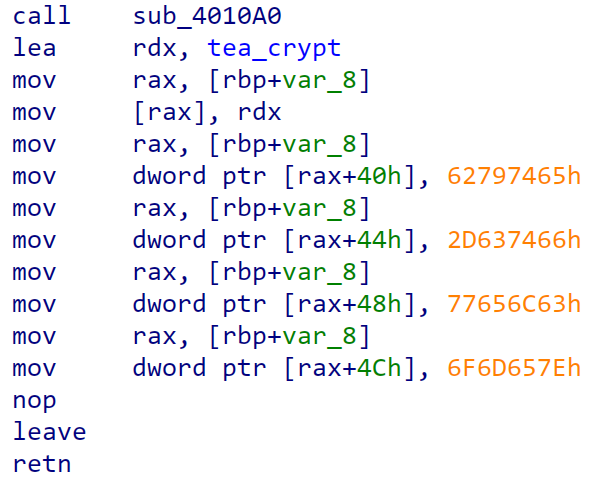
Comments

Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×